DragginMath: About Trees

DragginMath converts equations into interactive pictures. But these are not just any kind of picture. These pictures are called operator trees, and everything interesting about DragginMath has to do with them. That means your life will be easier if you learn a few words so we can talk about them.

In the usual mental picture of a tree, they grow and spread upward. But tree diagrams can be drawn in other directions, too. They might be drawn growing and spreading from left to right, or from right to left, or from top to bottom. For specific uses, you might prefer one of these directions over the others. But a tree’s connections don’t change regardless of which direction it grows, and it is only these connections that matter here.

In DragginMath, trees are drawn so they grow from top to bottom. We had to make a choice. This is it.

Trees are constructed from nodes and branches. In a DragginMath tree, nodes are drawn as rounded rectangles with math symbols inside. Branches are the swoopy lines that connect the nodes. The swoopiness of these lines doesn’t matter. We draw them that way because they look pretty. The length of a branch doesn’t matter. We try to make them so the pictures are simple and compact. Of course, it is possible to draw these diagrams with paper and pen, but computers do it more easily.

The node from which a tree grows is called its root, even if it is at the top of the picture. A tree can have only one root.

A really boring tree has no branches: it is just the root. It is important to note that boring trees like this can exist, and sometimes you might actually see them. But most trees have branches leading to other nodes, which can in turn lead to branches with even more nodes. In a tree diagram, branches can only spread out. They never come back together.

Any node at the far end of the branches is called a leaf. A tree can have many leaf nodes.

Other words that are useful are parent and child. A parent node is directly connected to a child node. In DragginMath, a parent is always drawn above a child. The root node of a tree can have children, but it has no parent. A leaf node has one parent, but it has no children. Nodes that are neither root nor leaf have no convenient name that is widely used. They are sometimes called internal nodes or intermediate nodes. Each of these has one parent and one or more children.

One can also talk about ancestors, descendants, and siblings.

Another important word is subtree. Any node in a tree is the root of its own subtree, which is a tree in its own right.

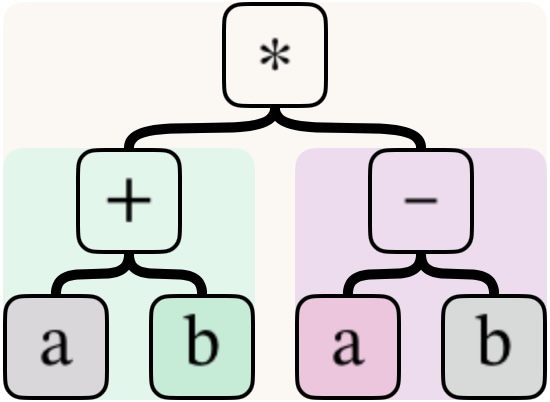
When discussing algebra in DragginMath, we often talk about nodes and branches, roots and leaves, parents and children, and subtrees. We need these words because algebraic expressions are in fact trees of operators (things like + − ∗ ÷) and operands (things like numbers and variables), even though they are traditionally written as a line of symbols. Understanding this is the start of your success in algebra. It is the reason DragginMath exists.

Operands are always leaf nodes; operators never are.

One of the major issues in teaching or learning algebra is operator precedence. This is the hierarchy of operators found in traditional math notation. Rather than having you look at a line of math symbols and hoping you can see the hierarchy in it, DragginMath simply shows you the hierarchy as an operator tree.